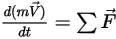
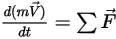
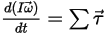
定义)，则该主体的平移运动将降为一个自由度 (1-DOF)。因此，根据线动量守恒，方程 2.426 将沿着运动方向变成标量方程，因为移动速度和力是由 
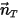表示的：
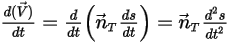
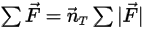
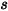是沿运动方向 
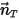运动的固体主体上某一关注点处位置矢量 
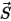的大小。在笛卡尔坐标系中，可得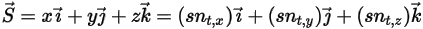
- 由压力和剪切力构成。它们是由流体流与接触流的固体主体曲面之间的相对运动引起的。压力和剪切力是通过流解 (输出量) 求得的：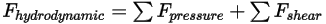
- 由摩擦阻尼作用引起的阻滞力。它是由固体对象的运动和用户定义的阻尼系数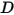 
确定的：
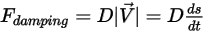
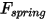- 由弦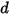 
的位移、弹簧常数 
和弹簧预紧力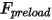 
来确定：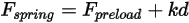
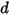的定义如下：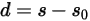
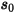是上一位置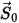 
处位置矢量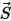 
的大小。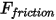
的建模如下：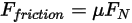
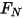是施加于所关注固体曲面的接触力的法向分量。针对摩擦系数 
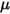，分别为静止主体和移动主体引入静态摩擦系数 
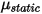和滑动摩擦系数 
：
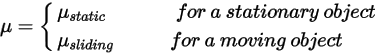
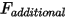- 添加用户指定的附加力。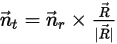
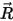是从轴中心指向固体主体上任意点 
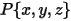的矢量：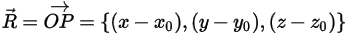
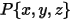处的角速度和扭矩可改写为：
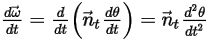
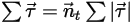
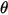是点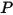 
相对于起始或参考位置的旋转角度。
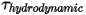- 由于压力和剪切力而产生的组合扭矩：
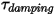- 由旋转速度 
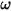和用户定义的阻尼系数 
来确定：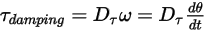
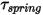- 由扭转引起的扭矩、位移角 
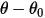、用户定义的预紧扭矩 
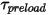以及扭转常数 
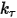来确定。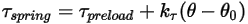
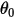是参考角。它通常是模型构建过程中边界或体积块所在的位置，但可以对应于不同的位置。例如，零角位移处的参考角 
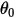与初始角度位置处的参考角不同。
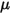和施加于接触曲面的法向力 
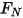所引起的接触扭矩：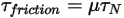
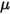是一个用户定义参数，其在方程 2.438 中定义。
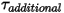- 添加用户指定的附加扭矩。
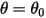从原始位置释放时，作用在其质量上的恢复力使其在平衡位置附近摆动。平衡位置 
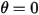任意一侧的最大角度取决于其释放位置 
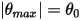。如果不存在摩擦 (无摩擦枢轴和真空)，则最大角度将保持不变，而摆锤会在相同的极值位置永久来回摆动。但是，例如当摆锤处于大气中时，空气阻力 (阻尼作用) 会导致最大摆角减小，并最终停止在平衡位置。
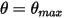时，它会随着其动能的总损失而改变方向。在此简易重力摆锤中，动能会完全转化为势能，而当考虑介质的阻力时，即会损失一部分动能来克服粘滞阻尼。但是，净力或势能会驱动摆锤开始在远离平衡位置的方向上运动，而当处于平衡位置时，动能 (速度) 最大，势能最小。在这种情况下，
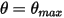表示 1-DOF 角动量 (方程 2.444) 的无反弹条件。
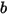和 
分别表示反弹和入射，以及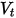 
和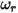 
分别表示平移和旋转速度 (仅限模) 时，此反弹模型的表示如下：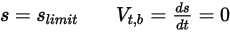
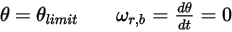
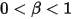) 而改变方向：
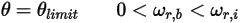
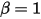) 的情况下改变方向：
是运动对象的质量；
⃗ 是线性/平移速度；而 
⃗ 是施加于平移主体的总力/净力。在
是惯性矩；
⃗ 是角速度；而 
⃗ 是作用在旋转体上的总扭矩/净扭矩。
和方向单位矢量 
定义时，固体主体绕轴 
的旋转也会降为 1-DOF 旋转。同样，根据角动量守恒，
，其定义如下：